Boundary interactions.

If the track processor determines that the photon has reached a boundary, then one of two things can happen - either it will be transmitted, or it will be reflected. In the current version of the code, Fresnel scattering is optional, but the total internal reflection criteria are not. These will determine where the photon goes next.

Given the unit vectors describing the direction of propagation and polarisation of the Cerenkov photon, the direction of the boundary normal, and the ratio of the refractive indices on the two sides of the boundary, the subroutine SPEC_REFL_PROB calculates and returns the probability of specular reflection and transmission at a boundary and DIFF_REFL_PROB does the corresponding job for diffuse reflection. The formulae for these probabilities may be found in most electromagnetism text books or, in the diffuse case come from optical measurements and best guesses. The only complication is that the formulae are couched in terms of the photon being polarised parallel or perpendicular to the plane of incidence, whereas the photons in question will usually be a mixture of the two. To overcome this the code calculates the overlap of the photon state with these two cases, and then randomly selects one or the other case dependant on the square of the overlaps. It then performs the calculations based on this selection.

If total internal reflection is indicated then the probability of reflection is set to one, and the subroutine immediately returns control to the calling routine. The Fresnel scattering routine may be switched off by using a flag in the MCMA titles bank. In this case the transmission probability is set to one - the possibility of total internal reflection will be dealt with by the routine REFRAC, when it determines that there is no possible, real, angle of transmission.

The subroutine REFRAC handles the geometry of where a Cerenkov photon goes when it is transmitted through the boundary.

Given a unit vector describing the direction of the incident photon, $\underline{\hat{a}}$, and the unit normal to the boundary^13.4, $\underline{\hat{n}}$, it can easily be shown that the direction of the reflected photon $\underline{\hat{b}}$ must lie in the plane defined by $\underline{\hat{a}}$ and $\underline{\hat{n}}$. Thus it is possible to write the direction of the refracted Cerenkov photon as a linear combination of these two vectors:

$$\underline{\hat{b}}= \alpha\underline{\hat{a}}+ \beta\underline{\hat{n}}$$ (13.3)

Using the conditions that 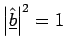$\left\vert \underline{\hat{b}} \right\vert^{2} = 1$, $\underline{\hat{a}}. \underline{\hat{n}}= \cos \theta_{i}$ and $\underline{\hat{b}} . \underline{\hat{n}}= \cos \theta_{t}$ where $\theta_{i}$ and $\theta_{t}$ are the angles of incidence and transmission respectively (as defined by Snell's law), and ignoring the solution that gives a negative value of $\alpha$, we get:

$$\alpha = \frac{n_{1}}{n_{2}} , \;\; \beta=\cos \theta_{t} - \alpha \cos \theta_{i}$$ (13.4)

where $n_{1}$, $n_{2}$ are the refractive indices on each side if the boundary. This solution is implemented in the code.

The subroutine SPEC_REFL handles the specular reflection of the Cerenkov photons at a boundary. The mathematics for this is similar to that discussed for REFRAC, except that the conditions to be applied in this case are 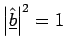$\left\vert \underline{\hat{b}} \right\vert^{2} = 1$ and that $\underline{\hat{a}}. \underline{\hat{n}}= - \underline{\hat{b}}. \underline{\hat{n}}$. Using these, it is possible to arrive at solutions for $\alpha$ and $\beta$:

$$\alpha=-1, \;\; \beta=0$$ (13.5)

$$\alpha=1, \;\; \beta=-2(\underline{\hat{a}}.\underline{\hat{n}})$$ (13.6)

The former solution may be ignored as it corresponds to the photon backtracking along its original path and, although it satisfies the conditions, is obviously not the desired solution. The latter solution is implemented in the code.