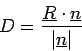


Next: Intersection of a line
Up: PMT-Reflector Geometry
Previous: Intersection of a line
Contents
The equation describing a right circular cone of radius
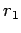 and height
and height 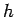 is given by
is given by
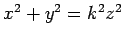 , where
, where 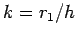 . The intersection
of a line with this cone lead to a quartic in
. The intersection
of a line with this cone lead to a quartic in  with solutions
of the form:
with solutions
of the form:
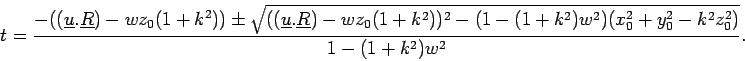 |
(13.3) |
In fact, this solution is valid only for an unbounded, infinite cone,
where the radius to height ratio at the point 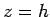 is given by
is given by 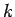 .
For the case of the frustum of cone, the cone is bounded and if the
intersection(s) is outside the planes defining the
top and bottom of the frustum of cone then the intersection(s)
with the plane(s) is given by
.
For the case of the frustum of cone, the cone is bounded and if the
intersection(s) is outside the planes defining the
top and bottom of the frustum of cone then the intersection(s)
with the plane(s) is given by
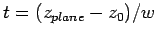 .
Provided
.
Provided 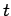 is positive, this can be used to form a proposed solution
is positive, this can be used to form a proposed solution
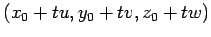 where the condition for intersection is that
where the condition for intersection is that
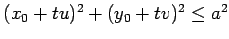 . In this case,
. In this case, 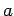 is equal to
is equal to 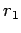 or
or
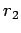 for the case of the top or bottom plane respectively.
for the case of the top or bottom plane respectively.
The normal to the curved sides of the frustum of cone is given
by 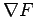 , where
, where 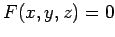 is the equation of a cone.
The (unormalized) normal to the cone at the point
is the equation of a cone.
The (unormalized) normal to the cone at the point 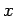 ,
, 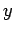 and
and 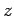 is then:
is then:
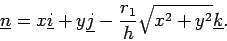 |
(13.4) |
Hence, the (signed) distance to the point
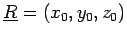 is just
is just
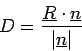 |
(13.5) |
and is the nearest distance from the point 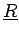 to
the curved sides of the frustum of cone for the case were
to
the curved sides of the frustum of cone for the case were
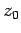 is between the planes defining the
top and bottom of the frustum of cone.
is between the planes defining the
top and bottom of the frustum of cone.



Next: Intersection of a line
Up: PMT-Reflector Geometry
Previous: Intersection of a line
Contents
sno Guest Acct
2009-09-09
![]() and height
and height ![]() is given by
is given by
![]() , where
, where ![]() . The intersection
of a line with this cone lead to a quartic in
. The intersection
of a line with this cone lead to a quartic in ![]() with solutions
of the form:
with solutions
of the form:
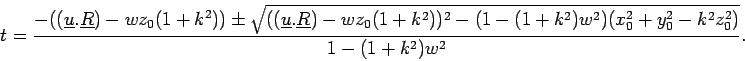
![]() , where
, where ![]() is the equation of a cone.
The (unormalized) normal to the cone at the point
is the equation of a cone.
The (unormalized) normal to the cone at the point ![]() ,
, ![]() and
and ![]() is then:
is then: