The most general torus is best described by an ellipse with semi-axes ![]() and
and
![]() , centred at
, centred at ![]() in the r-z plane (
in the r-z plane (
![]() ), which is
then rotated about the central axis of the torus (along the z-direction). The
equations describing the torus then become:
), which is
then rotated about the central axis of the torus (along the z-direction). The
equations describing the torus then become:
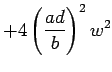 |
|||
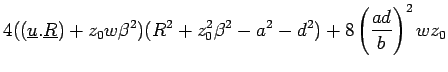 |
|||
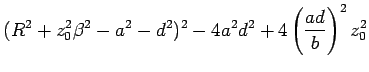 |
(13.9) |
| (13.10) |
Using the method of Cashwell and Everett [1], equation
13.8 may be solved to find all real solutions. The normal to a
surface described by the equation ![]() can be shown to be
can be shown to be ![]() .
From this, the (unnormalised) normal to an elliptical torus is found to be:
.
From this, the (unnormalised) normal to an elliptical torus is found to be:
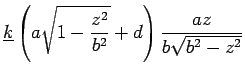 |
(13.11) |