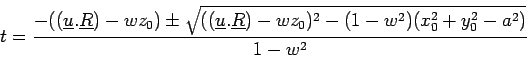


Next: Intersection of a line
Up: PMT-Reflector Geometry
Previous: Intersection of a line
Contents
The equation describing a right circular cylinder of radius 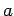 , aligned along
the z-axis, is
, aligned along
the z-axis, is
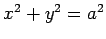 . The intersection of a line with this cylinder
will lead to a quadratic in
. The intersection of a line with this cylinder
will lead to a quadratic in 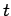 with solutions of the form:
with solutions of the form:
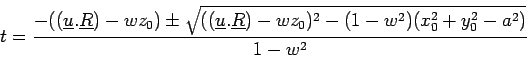 |
(13.2) |
This, of course, assumes an infinite length cylinder. If the cylinder is
bounded, then a check as to whether the predicted value of the z coordinate
lies within the bounds will show whether the intersection found using the above
equation is valid. A bounded cylinder also has ends, which also must be
checked. In this case the distance 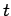 is defined:
is defined:
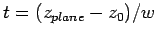 .
Provided
.
Provided 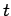 is positive, this can be used to form a proposed solution
is positive, this can be used to form a proposed solution
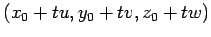 where the condition for intersection is that
where the condition for intersection is that
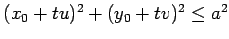 .
.
sno Guest Acct
2009-09-09
![]() , aligned along
the z-axis, is
, aligned along
the z-axis, is
![]() . The intersection of a line with this cylinder
will lead to a quadratic in
. The intersection of a line with this cylinder
will lead to a quadratic in ![]() with solutions of the form:
with solutions of the form: