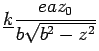


Next: How XED Works
Up: PMT-Reflector Geometry
Previous: Photomultiplier Geometry
Contents
In principle, the reflectors are Winston cones [2], although they
have been truncated somewhat to conform to the engineering requirements of the
SNO detector. In practise, as the surface of the Winston cone does not have a
tractable analytic form, they are modelled as a section of an elliptical torus.
The parameters of the torus are determined by fitting an ellipse to the profile
of the reflector, while the vertical sections are defined by the measured radii
at the top and bottom of the reflector.
The presence of 18 strips of `omega' (q.v.), known as `petals', further
complicates the model. They are modelled by assuming that the edges of the
petals lie along the shape of the reflector described above, but that the
petals are only bent in one direction, so that they are actually a section of
an elliptical cylinder, defined by these edges. Thus the procedure for
determining whether the reflector has been hit depends on solving the
intersection of a line with a torus, as discussed above, giving a `proposed'
solution  . This `proposed solution' can then be used to determine
which petal was hit, and from this the equation of the cylinder can be deduced
as follows. The number,
. This `proposed solution' can then be used to determine
which petal was hit, and from this the equation of the cylinder can be deduced
as follows. The number, 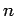 , of the petal is defined by the proposed solution
, of the petal is defined by the proposed solution
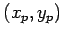 by extracting the angle
by extracting the angle
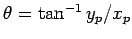 ;
; 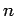 is then
the integer part of
is then
the integer part of 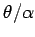 , where
, where
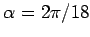 is the angular
width of one of the eighteen petals. The equation of the petal in the x-y plane
then becomes:
is the angular
width of one of the eighteen petals. The equation of the petal in the x-y plane
then becomes:
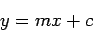 |
(13.12) |
where
However, 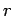 is not a constant, but a function of
is not a constant, but a function of 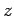 :
:
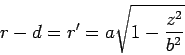 |
(13.15) |
which will give the equation of a cylinder of elliptical cross-section.
Solving for the intersection of a line with this elliptical cylinder will
give a solution of the form:
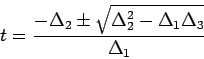 |
(13.16) |
where
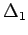 |
 |
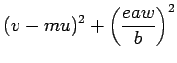 |
(13.17) |
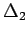 |
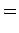 |
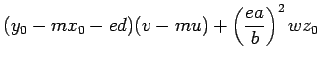 |
(13.18) |
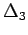 |
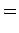 |
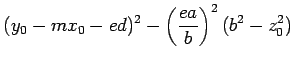 |
(13.19) |
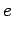 |
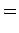 |
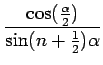 |
(13.20) |
Using the fact that 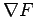 is the normal to the surface gives:
is the normal to the surface gives:
where 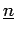 is not normalised.
is not normalised.



Next: How XED Works
Up: PMT-Reflector Geometry
Previous: Photomultiplier Geometry
Contents
sno Guest Acct
2009-09-09
![]() . This `proposed solution' can then be used to determine
which petal was hit, and from this the equation of the cylinder can be deduced
as follows. The number,
. This `proposed solution' can then be used to determine
which petal was hit, and from this the equation of the cylinder can be deduced
as follows. The number, ![]() , of the petal is defined by the proposed solution
, of the petal is defined by the proposed solution
![]() by extracting the angle
by extracting the angle
![]() ;
; ![]() is then
the integer part of
is then
the integer part of ![]() , where
, where
![]() is the angular
width of one of the eighteen petals. The equation of the petal in the x-y plane
then becomes:
is the angular
width of one of the eighteen petals. The equation of the petal in the x-y plane
then becomes:
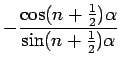
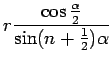
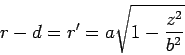
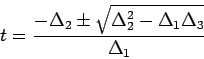
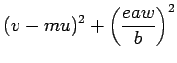
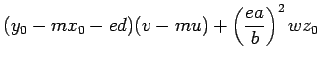
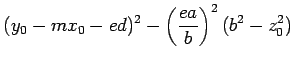
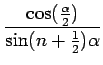
![]() is the normal to the surface gives:
is the normal to the surface gives: