Analyzing Backblaze’s Q3 2025 Stats
Last edited:
The Backblaze blog is awesome for finding out information about hard drives, especially if you are looking to build a NAS. They report quarterly information about the AFR, or annualized failure rate, of their hard drives grouped by hard drive model number. This metric is nice, but it doesn’t capture exactly what you want if you are looking to buy a reliable hard drive.
For example, a drive with 0 failures and 10,000 working hours will have an AFR of 0%, but a drive with 10 failures and 1,000,000 working hours will have a higher AFR of 0.4%. Intuitively we know that there is not enough data on the first drive to really know how reliable it is and so if I were building a NAS I would probably pick the second one. To capture this intuition, I re-analyzed the Backblaze Q3 2025 data and added two extra columns in addition to the AFR mode: the mean and the 95% limit. I also added it to a sortable HTML table so you can sort by whichever column you want.
Here is a short description of the columns:
- AFR (mode)
- This is what Backblaze reports as the AFR. It is the most likely value (mode) of the AFR posterior.
- AFR (mean)
- This is the mean of the AFR posterior. For drives with lots of stats and some failures this will be almost identical to the mode. However, for drives without any failures and not a lot of data, the posterior distribution will be asymmetric (see the plot at the bottom of this blog post) and the mode will be 0, but the mean more accurately measures the center of the distribution.
- AFR (95% limit)
- This is the value of the AFR which we are 95% sure that the real AFR is below. If you are looking to buy a known reliable hard drive, this seems like the number you would most care about.
| MFR | Model | Size (TB) | Drive Days | Fails | AFR (mode) | AFR (mean) | AFR (95% Limit) |
|---|---|---|---|---|---|---|---|
| WDC | WUH722222ALE6L4 | 22 | 3,555,491 | 50 | 0.51% | 0.52% | 0.65% |
| Toshiba | MG10ACA20TE | 20 | 1,416,127 | 21 | 0.54% | 0.57% | 0.78% |
| Seagate | ST16000NM001G | 16 | 3,125,133 | 57 | 0.67% | 0.68% | 0.83% |
| Toshiba | MG08ACA16TA | 16 | 3,686,376 | 85 | 0.84% | 0.85% | 1.01% |
| Seagate | ST12000NM001G | 12 | 1,219,082 | 31 | 0.93% | 0.96% | 1.25% |
| WDC | WUH721414ALE6L4 | 14 | 794,781 | 20 | 0.92% | 0.96% | 1.33% |
| Toshiba | MG07ACA14TA | 14 | 3,440,051 | 116 | 1.23% | 1.24% | 1.44% |
| Toshiba | MG08ACA16TE | 16 | 553,332 | 16 | 1.06% | 1.12% | 1.60% |
| Seagate | ST8000DM002 | 8 | 824,787 | 27 | 1.19% | 1.24% | 1.65% |
| Seagate | ST14000NM001G | 14 | 972,882 | 38 | 1.43% | 1.46% | 1.87% |
| Seagate | ST8000NM0055 | 8 | 1,224,440 | 53 | 1.58% | 1.61% | 1.99% |
| HGST | HUH721212ALE604 | 12 | 1,227,006 | 65 | 1.93% | 1.96% | 2.38% |
| HGST | HUH721212ALE600 | 12 | 239,677 | 9 | 1.37% | 1.52% | 2.39% |
| Seagate | ST12000NM000J | 12 | 91,723 | 2 | 0.80% | 1.19% | 2.51% |
| Seagate | ST16000NM002J | 16 | 42,581 | 0 | 0.00% | 0.86% | 2.57% |
| Seagate | ST12000NM0008 | 12 | 1,728,706 | 132 | 2.79% | 2.81% | 3.22% |
| Seagate | ST24000NM002H | 24 | 601,539 | 46 | 2.79% | 2.85% | 3.57% |
| WDC | WUH721816ALE6L0 | 16 | 274,775 | 20 | 2.66% | 2.79% | 3.86% |
| HGST | HUH728080ALE600 | 8 | 98,985 | 6 | 2.21% | 2.58% | 4.37% |
| Toshiba | MG11ACA24TE | 24 | 24,148 | 0 | 0.00% | 1.51% | 4.53% |
| Seagate | ST8000NM000A | 8 | 22,724 | 0 | 0.00% | 1.61% | 4.81% |
| HGST | HUH721212ALN604 | 12 | 912,361 | 109 | 4.36% | 4.40% | 5.11% |
| Toshiba | MG09ACA16TE | 16 | 17,852 | 0 | 0.00% | 2.04% | 6.12% |
| Toshiba | MG07ACA14TEY | 14 | 85,530 | 8 | 3.41% | 3.84% | 6.16% |
| HGST | HMS5C4040BLE640 | 4 | 17,194 | 0 | 0.00% | 2.12% | 6.36% |
| Seagate | ST500LM030 | 1 | 15,345 | 0 | 0.00% | 2.38% | 7.12% |
| Seagate | ST12000NM0007 | 12 | 91,835 | 13 | 5.17% | 5.56% | 8.21% |
| Toshiba | MQ01ABF050 | 1 | 12,017 | 0 | 0.00% | 3.04% | 9.10% |
| Seagate | ST14000NM0138 | 14 | 117,131 | 22 | 6.86% | 7.17% | 9.79% |
| Seagate | ST14000NM000J | 14 | 31,852 | 4 | 4.58% | 5.73% | 10.49% |
| Seagate | ST10000NM0086 | 10 | 91,650 | 20 | 7.97% | 8.36% | 11.57% |
| WDC | WUH721816ALE6L4 | 16 | 13,635 | 1 | 2.68% | 5.35% | 12.70% |
| Toshiba | MG08ACA16TEY | 16 | 462,943 | 215 | 16.95% | 17.03% | 18.98% |
Failure Model
In order to understand the raw data from Backblaze we need to start with a model for the failures of hard drives. A realistic model would be too complicated (see for example Backblaze’s blog post here), so we’ll stick with a very simple model. Let’s assume that each model of hard drive has a probability p of failing each day, and that each day the probability of failure is independent. We want to know: what is the probability for a failure rate p given that we had t total drive days and f failures, or equivalently:
\begin{equation}P(p|t,f) = \frac{P(t,f|p)P(p)}{P(t,f)}\end{equation}
We’ll assume the prior P(p) is flat, and the denominator is just a normalization constant, so we have:
\begin{equation}P(p|t,f) \propto P(t,f|p)\end{equation}
This latter expression is just equal to the probability of no failure for t-f days and failures on f days, i.e.
\begin{equation}P(t,f|p) = (1-p)^{t-f}p^f\end{equation}
Combining these last two expressions we get that the posterior for the failure rate p is proportional to:
\begin{equation} P(p|t,f) \propto (1-p)^{t-f}p^f \end{equation}
This is just the beta distribution with parameters:
\begin{align} \beta &= t-f+1 \\ \alpha &= f+1 \end{align}
This is nice because now we can compute all sorts of things about the posterior. For example, the mode (which backblaze reports as the AFR)
\begin{equation}\mathrm{AFR (mode)} = 365\cdot\frac{f}{t}\end{equation}
we can also calculate the mean:
\begin{equation}\mathrm{AFR (mean)} = 365\cdot\frac{f+1}{t+2}\end{equation}
Finally, we can calculate the 95% limit using the scipy.stats.beta distribution:
from scipy.stats import beta
a = f+1
b = t-f+1
p95 = 365*beta.ppf(0.95,a,b)It’s interesting to see how the posterior distribution changes over time. Here is a plot showing the posterior for the “Toshiba MG08ACA16TA” model after 1 day, 1 week, 1 month, and the full 3 months:
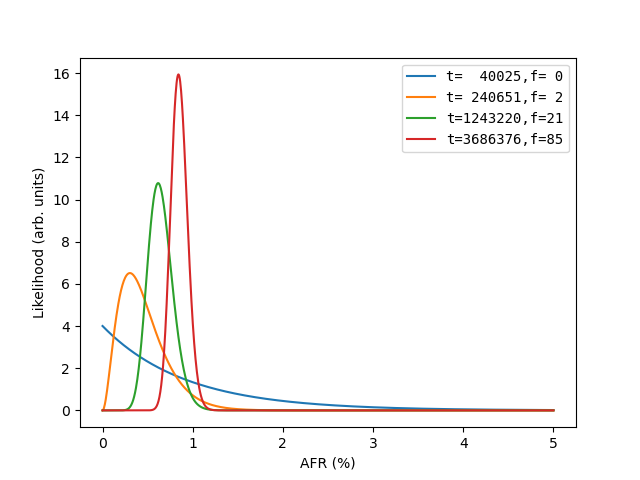
As you can see from the blue line the posterior starts out with a most likely AFR of 0% after 1 day (40,025 drive days), but the distribution has a significant fraction of it’s weight reaching all the way out to an AFR of more than 2%. After 1 week (240,651 drive days), there have been 2 failures and the distribution is still asymmetric but peaks somewhere just below an AFR of 0.5%. After 1 month (1,243,220 drive days) the distribution is starting to look Gaussian with a peak somewhere near 0.75%. Finally, after the whole quarter (3,686,376 drive days) the distribution still looks Gaussian but the peak has shifted closer to an AFR of 1%.
One cool thing about this visualization is we can kind of double check our assumptions. In this case we can see that although the peak shifted around quite a bit, all of the distributions had a significant fraction of their weight around the 1% AFR that it eventually settled in to, suggesting our initial assumption of a failure rate independent of time is probably good for this drive over this time period (at least with the amount of data we have).
Analyzing the Data
In order to analyze the data, I first downloaded the zip file containing all the csv files from Backblaze’s Hard Drive Test Data page. I then created an sqlite database with the relevant columns using the following schema:
CREATE TABLE IF NOT EXISTS backblaze_stats (
id INTEGER PRIMARY KEY,
date TEXT,
serial_number TEXT,
model TEXT,
capacity_bytes INTEGER,
failure INTEGER,
datacenter TEXT,
cluster_id INTEGER,
vault_id INTEGER,
pod_id INTEGER,
pod_slot_num INTEGER,
is_legacy_format TEXT
);Having the data in an SQLite database is nice because we can query the data by drive model and calculate the AFR all in a single command:
sqlite> SELECT model, SUM(failure) as failures, COUNT(*) AS drive_days, ROUND(365.0*SUM(failure)*100/COUNT(*),2) AS afr FROM backblaze_stats GROUP BY model ORDER BY drive_days DESC LIMIT 10;
model failures drive_days afr
-------------------- -------- ---------- ----
TOSHIBA MG08ACA16TA 85 3686376 0.84
WDC WUH722222ALE6L4 50 3555491 0.51
TOSHIBA MG07ACA14TA 116 3440051 1.23
ST16000NM001G 57 3125133 0.67
WDC WUH721816ALE6L4 64 2425374 0.96
ST12000NM0008 132 1728706 2.79
TOSHIBA MG10ACA20TE 21 1416127 0.54
HGST HUH721212ALE604 65 1227006 1.93
ST8000NM0055 53 1224440 1.58
ST12000NM001G 31 1219082 0.93